|
|
ナビエ・ストークスの方程式を導出しよう
 んじゃ、今回はナビエ・ストークスの方程式を見ていこう。オイラーの方程式まで到達するのはなんとかできたけど、ナビエ・ストークスの方程式がどう得られるのかいまいち分からずに、流体力学の授業が終わってしまった人、たくさんいるんじゃないかな?大学の授業でも詳しく導出までは触れないからね。だから、方程式を使っていろんな応用問題を解く際に、抵抗感をおぼえて不評なんじゃ。 んじゃ、今回はナビエ・ストークスの方程式を見ていこう。オイラーの方程式まで到達するのはなんとかできたけど、ナビエ・ストークスの方程式がどう得られるのかいまいち分からずに、流体力学の授業が終わってしまった人、たくさんいるんじゃないかな?大学の授業でも詳しく導出までは触れないからね。だから、方程式を使っていろんな応用問題を解く際に、抵抗感をおぼえて不評なんじゃ。
 じゃ、さっそくはじめようよ。でも、これを導出するのって、難しいんじゃない?
じゃ、さっそくはじめようよ。でも、これを導出するのって、難しいんじゃない?
 いや、そんなことないよ。心配はいらない。じゃが、導出までには、もちろんさまざまな予備知識が必要じゃ。じゃあ、さっそくその準備運動をしてみよう。面積力って知ってるかな? いや、そんなことないよ。心配はいらない。じゃが、導出までには、もちろんさまざまな予備知識が必要じゃ。じゃあ、さっそくその準備運動をしてみよう。面積力って知ってるかな?
 面積力って、面積に比例してちからが増えていく、そういう ちから のことよね。たとえば、私たちが慣れ親しんでいる圧力も、面積力よね。 面積力って、面積に比例してちからが増えていく、そういう ちから のことよね。たとえば、私たちが慣れ親しんでいる圧力も、面積力よね。
 あ、博士の考えていること、わかったよ。これからナビエ・ストークスの方程式を導出するにあたってぼく達が考えていかないといけない力は、圧力だけではない、なにか新しいタイプの面積力なんだよね。 あ、博士の考えていること、わかったよ。これからナビエ・ストークスの方程式を導出するにあたってぼく達が考えていかないといけない力は、圧力だけではない、なにか新しいタイプの面積力なんだよね。
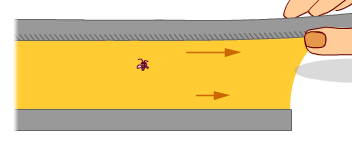
 たとえば下図のように、うすい板の上にハチミツをたらして、またその上に別の板を置いたとしましょう。上の板をスライドさせて動かしたとすると、板の面積が大きければ大きいほど、板の動きをさまたげるようにハチミツから受ける抵抗力は大きいわよね。この面積力って、はちみつに接している板の面に平行にはたらいているわ。ふつう、圧力だったら板の面に垂直にかかるはずだけどね。これこそニュータイプの「面積力」なのよね。 たとえば下図のように、うすい板の上にハチミツをたらして、またその上に別の板を置いたとしましょう。上の板をスライドさせて動かしたとすると、板の面積が大きければ大きいほど、板の動きをさまたげるようにハチミツから受ける抵抗力は大きいわよね。この面積力って、はちみつに接している板の面に平行にはたらいているわ。ふつう、圧力だったら板の面に垂直にかかるはずだけどね。これこそニュータイプの「面積力」なのよね。
 うむ、よく分かってるじゃないか。じゃあ、さっそくナビエ・ストークスの式をじっと眺めてみることにしよう(↓)。これは単位体積あたりの運動方程式をあらわしていることはもう分かってるよね?それが分からないなら、もうちょっと勉強しなおしてからこのページに挑戦しなくちゃならないけどね。じゃ、みんな分かってるとしよう。よく見れば、左辺も右辺も「単位体積あたりのちから」 [N/m3] で統一していることがすぐにわかる。右辺の第一項の単位は当然 [N/m3] じゃね。右辺の第二項をみてみよう。これも単位は [N/m3] のはず。ここで面積力となりうる「圧力」の p が登場しているが、面積力だけじゃ、単位体積あたりのちからにはなっていないことに注意しよう。 うむ、よく分かってるじゃないか。じゃあ、さっそくナビエ・ストークスの式をじっと眺めてみることにしよう(↓)。これは単位体積あたりの運動方程式をあらわしていることはもう分かってるよね?それが分からないなら、もうちょっと勉強しなおしてからこのページに挑戦しなくちゃならないけどね。じゃ、みんな分かってるとしよう。よく見れば、左辺も右辺も「単位体積あたりのちから」 [N/m3] で統一していることがすぐにわかる。右辺の第一項の単位は当然 [N/m3] じゃね。右辺の第二項をみてみよう。これも単位は [N/m3] のはず。ここで面積力となりうる「圧力」の p が登場しているが、面積力だけじゃ、単位体積あたりのちからにはなっていないことに注意しよう。
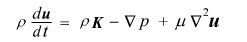
 うん。圧力の勾配を取ってるよね。単位という視点で考えると、(圧力)÷(距離)の演算だね。 うん。圧力の勾配を取ってるよね。単位という視点で考えると、(圧力)÷(距離)の演算だね。
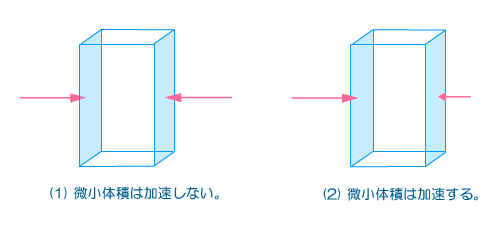
 そう。圧力などの「面積力」は、それだけでは微小な物体を動かす(加速する)ちからにはなりえない。なぜなら、微小な物体の一つの面にいくら大きな面積力がかかっていても、逆側の面にも等しく大きな力がかかっていたら、動きようがないからじゃ。つまり、微小体積を動かしたいとき、どこでも等しい圧力じゃダメで、たとえば x 方向に動いたら圧力が変わるようにしなくちゃならないね。だから勾配をとっているわけじゃね。 そう。圧力などの「面積力」は、それだけでは微小な物体を動かす(加速する)ちからにはなりえない。なぜなら、微小な物体の一つの面にいくら大きな面積力がかかっていても、逆側の面にも等しく大きな力がかかっていたら、動きようがないからじゃ。つまり、微小体積を動かしたいとき、どこでも等しい圧力じゃダメで、たとえば x 方向に動いたら圧力が変わるようにしなくちゃならないね。だから勾配をとっているわけじゃね。
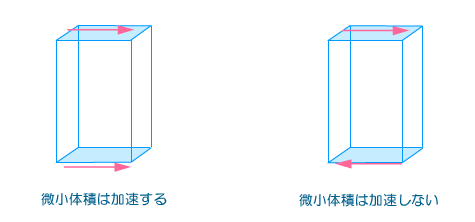
 そっか、てことは、同じ面積力である「せん断応力」についてもそうで、微小体積を動かすには、せん断応力が場所によってに違いが生まれなきゃいけないのね。下の図でしめしたように、合計で右方向にちからがかかっていることになれれば加速できるわね。偶力になっているケースでは、左右で同じ力が逆向きに働くから、結局合計ではゼロになって右にも左にも加速できないことになるのね。 そっか、てことは、同じ面積力である「せん断応力」についてもそうで、微小体積を動かすには、せん断応力が場所によってに違いが生まれなきゃいけないのね。下の図でしめしたように、合計で右方向にちからがかかっていることになれれば加速できるわね。偶力になっているケースでは、左右で同じ力が逆向きに働くから、結局合計ではゼロになって右にも左にも加速できないことになるのね。
 ふむふむ、わかったぞ。ひょっとして、今まで分からなかったナビエ・ストークスの方程式が今のヒントで理解できるかもしれない。簡単のため、二次元のナビエ・ストークスの方程式を考えるとして、教科書からその式をまず書き下してみよう。 x 方向の速さ u についてのナビエ・ストークスの方程式については、「 y 方向にちょっと動いたときに、どれくらい面積力の差がでてくるか」を考えてやればいいね。ちょっと x 方向だけについて書き下してみよう。きっと、面積力を y で偏微分したような形がでてくるはず、、、 ふむふむ、わかったぞ。ひょっとして、今まで分からなかったナビエ・ストークスの方程式が今のヒントで理解できるかもしれない。簡単のため、二次元のナビエ・ストークスの方程式を考えるとして、教科書からその式をまず書き下してみよう。 x 方向の速さ u についてのナビエ・ストークスの方程式については、「 y 方向にちょっと動いたときに、どれくらい面積力の差がでてくるか」を考えてやればいいね。ちょっと x 方向だけについて書き下してみよう。きっと、面積力を y で偏微分したような形がでてくるはず、、、
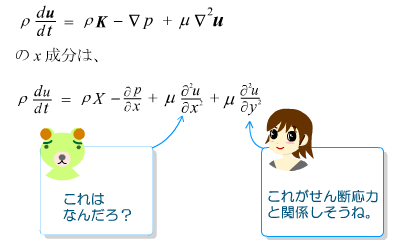
 うーむ、困ったぞ。たしかに y で偏微分している項はあるな。これはせん断応力によるものなんだろうか?ほかにも x で偏微分している項もあるね。これはなんだろう。 うーむ、困ったぞ。たしかに y で偏微分している項はあるな。これはせん断応力によるものなんだろうか?ほかにも x で偏微分している項もあるね。これはなんだろう。
 ほっほっほ。なかなか一筋縄ではいかないようじゃの。でも、くまきちもみいさんも、いい筋しとるぞ。実は垂直応力についても考えていかなきゃならんだけで、せん断応力についての考え方はそれでよいんじゃ。では、これからはムービーを使って、じっくりと導出していこう。 ほっほっほ。なかなか一筋縄ではいかないようじゃの。でも、くまきちもみいさんも、いい筋しとるぞ。実は垂直応力についても考えていかなきゃならんだけで、せん断応力についての考え方はそれでよいんじゃ。では、これからはムービーを使って、じっくりと導出していこう。
|
 |
   
これで解決!ナビエ・ストークスの方程式解説ムービー
(Windowsのみ) 所要時間:90分
ナビエ・ストークスの方程式は、粘性のある流体に関する運動方程式です。せん断応力や、垂直応力を加味して、粘性のない場合、つまりオイラーの方程式を発展させたものが、このナビエ・ストークスの方程式です。せん断応力、垂直応力はどのようにして発生するのか、どの方向に発生しているのか、などを詳しく調べていき、最終的にナビエ・ストークスの方程式にたどりつきます。
まずは、ムービー(無料)を見ながら練習問題1を解いていきましょう。ムービーへはこちらをクリック!(要Flash Player) 第一章まで無料で楽しめます。
|
 |
 第一章までの無料のムービーはこちらへどうぞ。(音声はありません。) 全てをご覧頂くには、ご購入いただく必要があります。 第一章までの無料のムービーはこちらへどうぞ。(音声はありません。) 全てをご覧頂くには、ご購入いただく必要があります。

クリックして早速見てみよう!
|
 |
 スクリーンショット スクリーンショット

|
|

