|
|

これで解決!偏微分-連鎖律とヘッセ行列 解説ムービー
(Windowsのみ) 所要時間:50分
接平面と勾配の巻をマスターしたら、今度は微分の連鎖律とヘッセ行列に挑戦してみよう。どちらも偏微分を理解したり使いこなすには必須だよ!
●ニ変数の関数の極大、極小、鞍点の判別がいまいちしっくりこない。どうしてヘッセ行列のようなものが必要なのだろう。
●どうして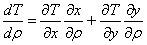 みたいに多変数の偏導関数の求め方はややこしいの?法則が理解できない。少し変則的な偏微分の導出になると、太刀打ちできない。 みたいに多変数の偏導関数の求め方はややこしいの?法則が理解できない。少し変則的な偏微分の導出になると、太刀打ちできない。
などなど、そんな疑問を持つ人にオススメです!
じっくりと例題を解きながら、手抜きなし!確実な理解をものにするために、頭のよくないくまきちたちと一緒にゆっくり進んでいきます。ムービーへはこちらをクリック!(要Flash Player)有料です。
|
 詳しい授業内容
詳しい授業内容
この授業で重点的に取り上げる項目は以下の通りです。
・偏微分の連鎖律chain rule
簡単な偏微分の計算が出来ていても、他の媒介変数が登場したら直ぐに混乱してしまう人が対象です。間違いの少ない機械的な方法で理解を目指します。また、天下りに公式を覚えるのではなく、なぜchain
ruleが必要なのかを分析しながら進めていきます。そして、実際の曲面と照らし合わせながら、直感的な理解で補完していきます。
・ヘッセ行列------関数の最大値と最小値
最大値、最小値を求めるときになぜヘッセ行列が必要なのかが理解できない人のための項目です。極値を持つ時と、鞍点を持つときの決定的な違いについて説明。例題を2問解きながらじっくり取り組んでいきましょう。 |
 |
 スクリーンショット スクリーンショット
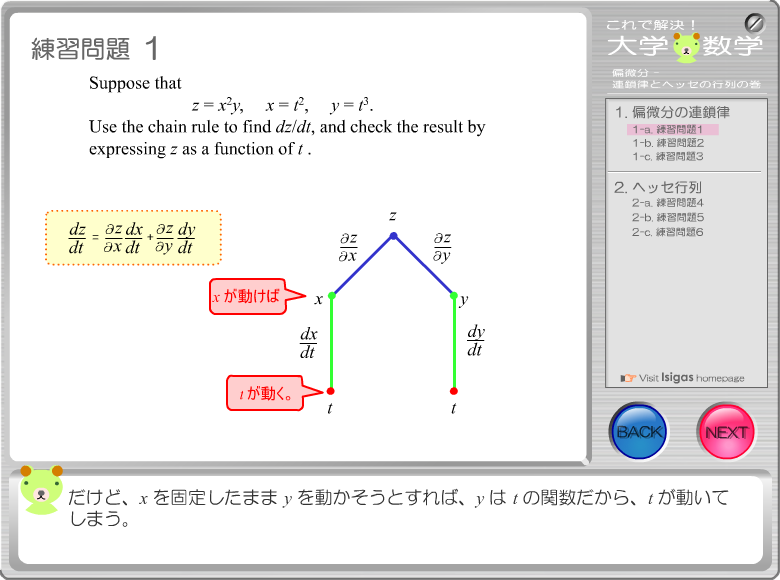
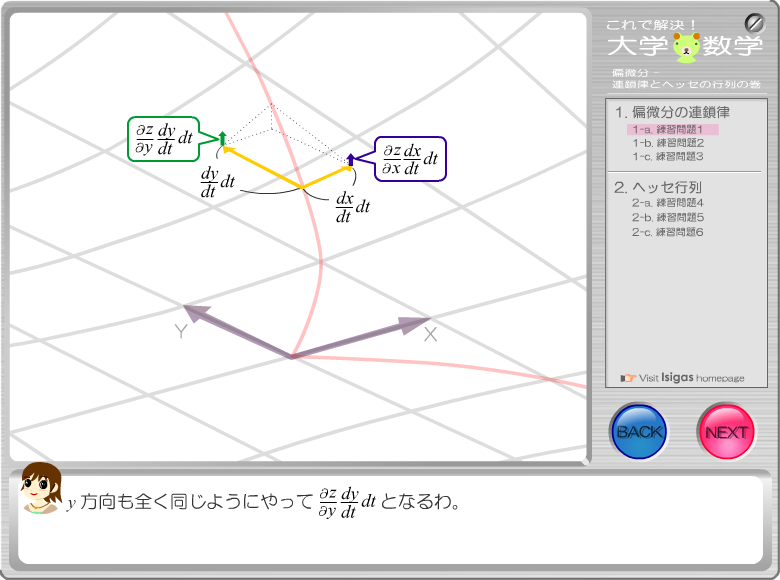
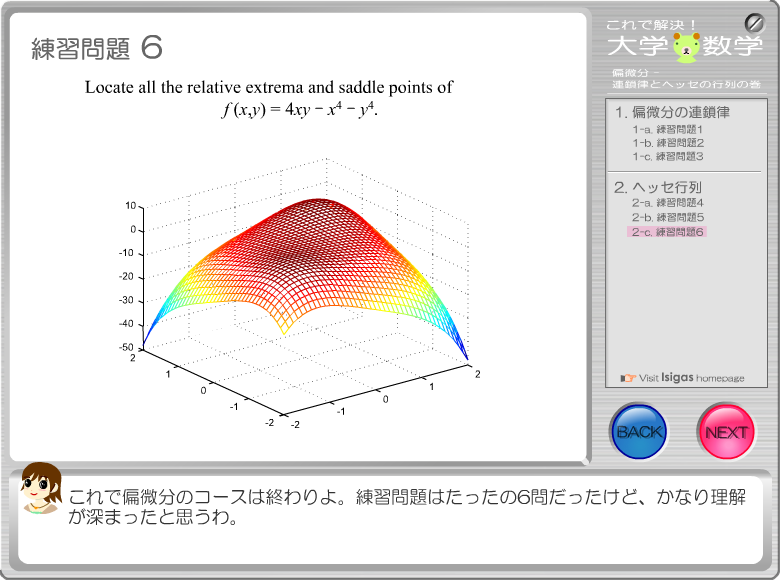
|
|
|

