|
|
テイラー展開を図解してみよう
 んじゃ、今回はテイラー展開を見ていこう。なんとなくわかるけど、テイラー展開がどうも感覚的につかめない、なんてことはないかな?数式を使って示す方法は有名だけれども、幾何的にわかりやすく説明できたらうれしいね。 んじゃ、今回はテイラー展開を見ていこう。なんとなくわかるけど、テイラー展開がどうも感覚的につかめない、なんてことはないかな?数式を使って示す方法は有名だけれども、幾何的にわかりやすく説明できたらうれしいね。
 じゃ、さっそくはじめようよ。下の図で見るとおり、(x0, f (x0))の点を基準にとって、そこからx 方向にh だけ進んだら、 f (x)の値がどのくらい変わるか知りたい。それを図の中で”?”マークであらわしている。
じゃ、さっそくはじめようよ。下の図で見るとおり、(x0, f (x0))の点を基準にとって、そこからx 方向にh だけ進んだら、 f (x)の値がどのくらい変わるか知りたい。それを図の中で”?”マークであらわしている。
ここで、導関数を導入してみよう。(x0, f (x0))の点から単位距離 1 だけ x 方向に進んだら、 y 方向に a だけ増加するような割合でこの関数がかたむいているとしよう。その a が一階の導関数 f '(x0)であることは オーケー だよね。
 上の図をみるとわかるように、 x 方向に動いた量 h を n 分割するとしましょう。そうすると、分割されたひとつひとつの長さは h/n になるね。その動いた距離に応じてそれに a を掛けた値が y 方向に増える量よね。 上の図をみるとわかるように、 x 方向に動いた量 h を n 分割するとしましょう。そうすると、分割されたひとつひとつの長さは h/n になるね。その動いた距離に応じてそれに a を掛けた値が y 方向に増える量よね。
今回、x方向に h だけ動いて、それに応じて y 方向に増える量は ha となるよ。 よって、上の図での "?" の高さは下の式のようになる。もちろん、これだけではまだ真の値に少しちかづいただけね。
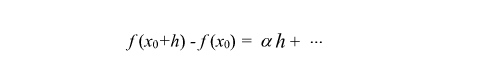
 さて、いよいよ次に二階の導関数を考えてみましょう。なぜかっていうと、さっき、一次導関数によって求まった高さの変化は直線的なものと近似したから、本当の f (x)の変化には完全には追従できていないからね。ちょっと誤差が生じてしまっている。この誤差分を二次近似で埋めていくのね。 さて、いよいよ次に二階の導関数を考えてみましょう。なぜかっていうと、さっき、一次導関数によって求まった高さの変化は直線的なものと近似したから、本当の f (x)の変化には完全には追従できていないからね。ちょっと誤差が生じてしまっている。この誤差分を二次近似で埋めていくのね。
二次導関数を考慮するってことは、一次導関数がどんどん増えていくって考えることができるわよね(二次導関数が正のとき)。一階の導関数、つまり赤の箱の高さが一定の割合で増えていく、、ってことを意味しているよね。下の図の緑色の箱がその割合を示しているわよ。これらをどんどんたして、赤い箱の高さがどんどん高くなっていくことを確認しようね。下の図では、x0 + h まで進んだときに、緑色の箱の高さが1+2+3 = 6こ分、足されて高くなっていることがわかるね。この増加分が、二階導関数をかんがえたときの増加分だよ。
 この緑色の箱ひとつひとつの高さを実際に求めてみましょう。二階導関数の定義にもどって考えてみると、、、下の式において、dx → 0としたときが二階導関数なんだけど、 この緑色の箱ひとつひとつの高さを実際に求めてみましょう。二階導関数の定義にもどって考えてみると、、、下の式において、dx → 0としたときが二階導関数なんだけど、
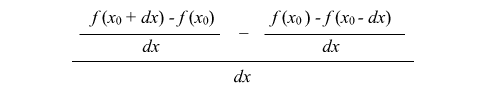
この式を b と置くと、 b において、次の式が得られるよ。
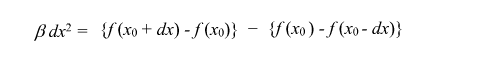
上式の右辺が緑箱の一個の高さ(図において、dx = h/n と考えてね。)なんだから、bdx2 = b(h/n)2 が、緑箱の高さだってことになるね。
 このときって、緑色の箱が積み重なることによってできる箱の高さは、x0 + h の地点ではどうなるのかしら。一個一個の箱の高さは bh2/n2 なので、それが 1+2+3+…n = n(n+1)/2 個なんだから、計算すると、下の式を得るわ。
このときって、緑色の箱が積み重なることによってできる箱の高さは、x0 + h の地点ではどうなるのかしら。一個一個の箱の高さは bh2/n2 なので、それが 1+2+3+…n = n(n+1)/2 個なんだから、計算すると、下の式を得るわ。
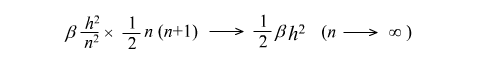
 やっと到達したね。二階導関数を導入したことによって増えた高さは (1/2)bh2だ! やっと到達したね。二階導関数を導入したことによって増えた高さは (1/2)bh2だ!
 はっはっは。よくやったね。では、三階の導関数を導入するとしたら、どのようになるかな? はっはっは。よくやったね。では、三階の導関数を導入するとしたら、どのようになるかな?
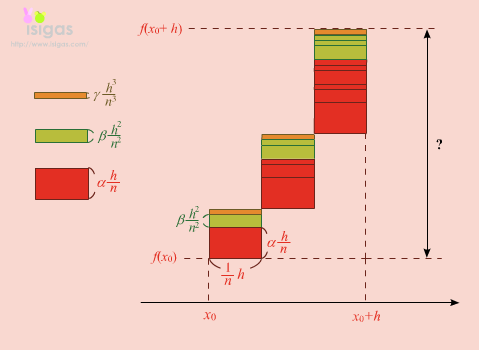
 こんどは、二階導関数が一定の割合で増えていくんだね。だから、緑の箱の高さがどんどん増えていくような図を考えていけば解けるよ。二階導関数のとき、一個のブロックの高さが b (h/n)2 であたえられていたから、三階では g (h/n)3 となるんじゃないかな。(今回、証明は省きます。) こんどは、二階導関数が一定の割合で増えていくんだね。だから、緑の箱の高さがどんどん増えていくような図を考えていけば解けるよ。二階導関数のとき、一個のブロックの高さが b (h/n)2 であたえられていたから、三階では g (h/n)3 となるんじゃないかな。(今回、証明は省きます。)
 三階導関数によって増える高さは、この上のブロック図でながめると、 h の幅が3分割されているから1+3+6 = 10 個分だけれども、 h の幅をもっともっとたくさん分割して n 個に分割したとすると、1+3+6+10+… = ?? どうなるのかしら?(↓) 三階導関数によって増える高さは、この上のブロック図でながめると、 h の幅が3分割されているから1+3+6 = 10 個分だけれども、 h の幅をもっともっとたくさん分割して n 個に分割したとすると、1+3+6+10+… = ?? どうなるのかしら?(↓)
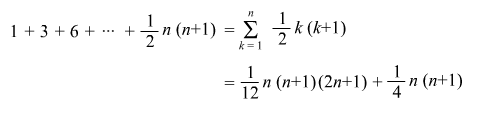
 ちょっと迷ったけど、高校の知識でなんとかなるわ。数列の和の公式に代入して一発よ。さて、では合計の高さは、上で得られた式に g (h/n)3 を掛けて、、、(↓) ちょっと迷ったけど、高校の知識でなんとかなるわ。数列の和の公式に代入して一発よ。さて、では合計の高さは、上で得られた式に g (h/n)3 を掛けて、、、(↓)
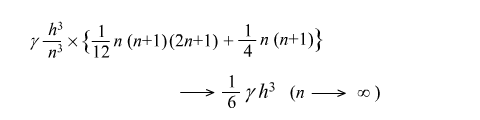
 できた。これで、三階導関数も考慮したときの高さの変化が求められて…(↓) できた。これで、三階導関数も考慮したときの高さの変化が求められて…(↓)
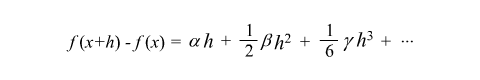
 のようになるね。で、a = f '(x0), b = f "(x0), g = f (3)(x0) を代入すれば、テイラー展開の式が導けたとなる。ひゃー、疲れた。でも、図形的にテイラー展開の式を導けた、っていうのは、意義があることだとおもうよ。 のようになるね。で、a = f '(x0), b = f "(x0), g = f (3)(x0) を代入すれば、テイラー展開の式が導けたとなる。ひゃー、疲れた。でも、図形的にテイラー展開の式を導けた、っていうのは、意義があることだとおもうよ。
 ほっほっほ。どうじゃったかな? ほっほっほ。どうじゃったかな?
|
 |
|

