|
|
対流項（移流項）をかんがえよう
 流体力学をこれから学ぼうという人は必須だよ。対流項（移流項）についての解説がどっさり。非常に詳しくて、しかも初学者のことを考えた授業が進んでいくよ。ムービーを用いて、対流項（移流項）を含んだ波がどんな発展をしていくかを見たりして、視覚的、感覚的にもセンスを磨いていこう。
 ねぇ、その対流項（移流項）ってやつ、どれのことを指しているの？
たとえば、下に示した数式の右辺第二項じゃ。速さとナブラの内積があって、それにある物理量（今回はu）が右からかかっている。
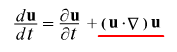
 全微分と偏微分をつなぐ式、といってもいいよね。てことは、この対流項を理解していないと、全微分も偏微分も理解していたとはいえない、ともいえるんじゃないかな。
いままで、この対流項の計算問題でまちがちゃった人、多いんじゃないかな？そして、そもそもこの式の意味していることをしっかり理解するには、やはりそれなりに時間を割いて、深くかんがえていかねばならん。このムービーを見終わったら、計算問題につまづかないだけじゃなくて、本質的な理解も進んで一石二鳥じゃ。流体力学をこれから学ぶ人はぜひマスターしてほしい。さっそく、ムービーを見てみようか。
え？もうぼくたちの会話は終わり？なんか、今回の紹介は手抜きじゃない？
うふふ。ムービーを見てのお楽しみってことにしましょうよ。
|
 |
これで解決！対流（移流項）解説ムービー
(Windowsのみ) 所要時間：60分
1.コメ農家になって、対流項を理解しよう：実際に例題をあげながら、それを考える必要がある理由を考えましょう。そして、近似曲面を用いた全微分の式から、対流項を導出します。
2.連鎖律を用いて考える：同じ導出を連鎖律の接続木を用いて考えていきます。xだけじゃなく、yやzと次元が増えていったとき、どう数式で表現できるのか、みていきましょう。
3.河口での潮の満ち干き：コメ農家に引き続き、対流項が活躍するケースをもうひとつ取り上げます。河口にてじっとしているイボニシ（貝のなかま）くんと、ウナギくんが感じる塩の濃度について見ていきましょう。潮が満ちてきたり、雨が降ってきたりした場合、偏微分の項や対流項にどんな変化があらわれるかを考えていきます。
4.計算問題：ただの計算問題ですが、ところがどっこい、引っかかってしまう人が続出。気をつけて解いていきましょう。解説付き。
5.運動方程式：対流項は運動方程式の中によく登場します。実際にそのケースについて見ていきます。
6.高調波のあらわれ：演習を一問いっしょに解いていきながら、高調波を生み出す対流項の特徴について考えていきましょう。高調波はどうして生まれてしまうのかな？
7.非粘性Burgers方程式：この方程式は、対流項が登場する非常に簡単な方程式です。対流項がどのような性質を持っているかをとらえるのに、最適です。コンピュータグラフィクスを用いて、実際に波形がどのように変化していくのかを追いながら、観察していきます。結果として衝撃波が生じるところまで学びましょう。
8.Burgers方程式：拡散項が足された式、Burgers方程式を比較対象にして、拡散項がどのような働きをしているのかを見ていきます。Burgers方程式はKorteweg-de Vries方程式(K-dV方程式)を学ぶにあたって避けては通れません。K-dV方程式について知らない人も、対流項、偏微分の項、拡散項について深く知りたいならばオススメです。
|
|
第二章までの無料のムービーはこちらへどうぞ。（音声はありません。） 全てをご覧頂くには、ご購入いただく必要があります。
クリックして早速見てみよう！
|
|
スクリーンショット
第二章 連鎖律を用いてかんがえる
第三章 河口での潮の満ち干き
第四章 計算問題
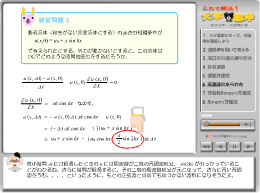
第六章 高調波のあらわれ
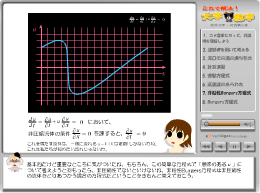
第七章 非粘性Burgers方程式
|
|
公開中の授業
