|
|
複素積分の前に、まずは準備体操
 複素積分ってぶっちゃけていうと、わりあい簡単じゃない?留数を求めてやればなんとかなる、みたいな傾向があるのよね。 複素積分ってぶっちゃけていうと、わりあい簡単じゃない?留数を求めてやればなんとかなる、みたいな傾向があるのよね。
 うん、でもさ、実際にどれだけぼくたちが複素積分を理解できたかというと、いまいちしっくりこないんだよ。そもそも、複素関数のはじめのほうにでてくるコーシー・リーマンの方程式すらあんまり分かっていないんだよね。やっぱり感覚的にイメージできないのが致命的だよ。 うん、でもさ、実際にどれだけぼくたちが複素積分を理解できたかというと、いまいちしっくりこないんだよ。そもそも、複素関数のはじめのほうにでてくるコーシー・リーマンの方程式すらあんまり分かっていないんだよね。やっぱり感覚的にイメージできないのが致命的だよ。
 そうよね。急にコーシー・リーマンの方程式が登場して、「覚えなさい」なんていわれているような気がするのよ。 そうよね。急にコーシー・リーマンの方程式が登場して、「覚えなさい」なんていわれているような気がするのよ。
 んじゃさ、複素積分については本ムービーでかんがえるとして、ここでは予習として、複素関数の微分をまじえてコーシー・リーマンの方程式についてかんがえてみない? んじゃさ、複素積分については本ムービーでかんがえるとして、ここでは予習として、複素関数の微分をまじえてコーシー・リーマンの方程式についてかんがえてみない?
 賛成~。じゃ、そのためには微分可能性についてざっと復習してからにしましょうよ。複素関数では、下にあらわす極限値が z の近づく方向にかかわらず(どのようにz0に近づいても)、同じ値をもつことが微分可能であるために必要だって教科書はいうのよね。 賛成~。じゃ、そのためには微分可能性についてざっと復習してからにしましょうよ。複素関数では、下にあらわす極限値が z の近づく方向にかかわらず(どのようにz0に近づいても)、同じ値をもつことが微分可能であるために必要だって教科書はいうのよね。
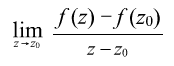
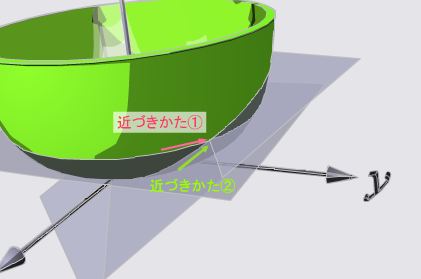
 うん。ぼくなんか、そういうのあんまりくわしく考えたことないよ。ただ、高校で習った微分の式で、x を z におきかえただけ、っていう風におぼえてる。でもさ、「ある値 z0 に近づいていくときに、どういう近づき方でも同じ値だったら微分可能」って、よく考えると変な話だよ。たとえば z(x, y) = x2 + y2 なんていう関数を考えたとするじゃない?つまり、偶然ながら z は実数関数だとする。 z を高さで表せば、お椀のかたちをした曲面になるよね。 うん。ぼくなんか、そういうのあんまりくわしく考えたことないよ。ただ、高校で習った微分の式で、x を z におきかえただけ、っていう風におぼえてる。でもさ、「ある値 z0 に近づいていくときに、どういう近づき方でも同じ値だったら微分可能」って、よく考えると変な話だよ。たとえば z(x, y) = x2 + y2 なんていう関数を考えたとするじゃない?つまり、偶然ながら z は実数関数だとする。 z を高さで表せば、お椀のかたちをした曲面になるよね。
 そうすると、近づき方によって、かたむきなんて変わっちゃう。ほら、下を見て。近づき方①と②では、さっそく かたむきが違うじゃない。どういう近づきかたでも同じ値といったら、z(x, y) = x2 + y2の場合には原点しかないじゃない! そうすると、近づき方によって、かたむきなんて変わっちゃう。ほら、下を見て。近づき方①と②では、さっそく かたむきが違うじゃない。どういう近づきかたでも同じ値といったら、z(x, y) = x2 + y2の場合には原点しかないじゃない!
 原点以外微分不可能ってことになるよね。なんだか不思議だな。実は、この微分可能性についての条件って、けっこう厳しい条件なんじゃない? 原点以外微分不可能ってことになるよね。なんだか不思議だな。実は、この微分可能性についての条件って、けっこう厳しい条件なんじゃない?
 おやおや、やっとるな。くまきち、そのとおりじゃよ。普通の実数関数を複素関数ととらえた場合、一般的にはどの点においても微分可能ではない。 おやおや、やっとるな。くまきち、そのとおりじゃよ。普通の実数関数を複素関数ととらえた場合、一般的にはどの点においても微分可能ではない。
 あ、ドクター博士! やっぱりそうなんだ。なんだか複素関数って不思議な関数だね。 あ、ドクター博士! やっぱりそうなんだ。なんだか複素関数って不思議な関数だね。
 じゃ、例として次の複素関数をみていこうか。かなり簡単な関数じゃが、例としては最適じゃよ。この関数は微分可能だぞ。 じゃ、例として次の複素関数をみていこうか。かなり簡単な関数じゃが、例としては最適じゃよ。この関数は微分可能だぞ。
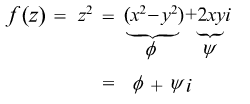
 この関数を微分すると、f '(z) = 2zになるのよね。ある意味、高校時代に習った微分と同じように計算できるから、ラクだわ。 この関数を微分すると、f '(z) = 2zになるのよね。ある意味、高校時代に習った微分と同じように計算できるから、ラクだわ。
 こういうとき、f(z)って一体なんなんだろう?なにか曲線で表されるのかな? こういうとき、f(z)って一体なんなんだろう?なにか曲線で表されるのかな?
 でもね、教科書をみると、コーシー・リーマンの方程式くらいしか載っていないのよ。これからなにか分かるのかしら? でもね、教科書をみると、コーシー・リーマンの方程式くらいしか載っていないのよ。これからなにか分かるのかしら?
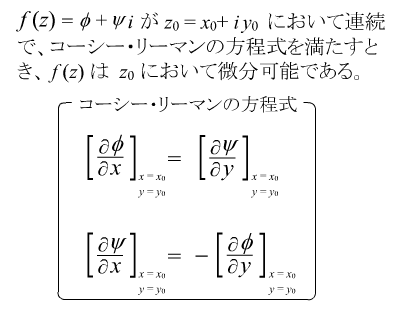
 でもさ、ここでコーシー・リーマンの方程式を出されると、少しこまっちゃうんだな。ただの無味乾燥な式に見える。 でもさ、ここでコーシー・リーマンの方程式を出されると、少しこまっちゃうんだな。ただの無味乾燥な式に見える。
 何が? 何が?
 これって、x軸から近づいても、y軸から近づいても、f(z)の偏微分はある同じ値にちかづきますよ、っていう式から求められるんだよね。じゃあ、そういうときには、φとかψはどういう関数になるべきなんだろう。つまり、微分可能な複素関数ってどんな関数なんだろう。式じゃなくて感覚で知りたいんだ。f(z) = z2 だったら、φ = x2- y2とψ = 2xyにどういう関係があるんだろう?? これって、x軸から近づいても、y軸から近づいても、f(z)の偏微分はある同じ値にちかづきますよ、っていう式から求められるんだよね。じゃあ、そういうときには、φとかψはどういう関数になるべきなんだろう。つまり、微分可能な複素関数ってどんな関数なんだろう。式じゃなくて感覚で知りたいんだ。f(z) = z2 だったら、φ = x2- y2とψ = 2xyにどういう関係があるんだろう??
 ひょっとして、それぞれの等高線がcurvilinear squaresを形成しているってことを知りたい?? ひょっとして、それぞれの等高線がcurvilinear squaresを形成しているってことを知りたい??
 curvilinear squaresって?? curvilinear squaresって??
 では、実際にf(z) = z2 だとして、φ = x2- y2 とψ = 2xyを描画してみよう。ほれ。 では、実際にf(z) = z2 だとして、φ = x2- y2 とψ = 2xyを描画してみよう。ほれ。
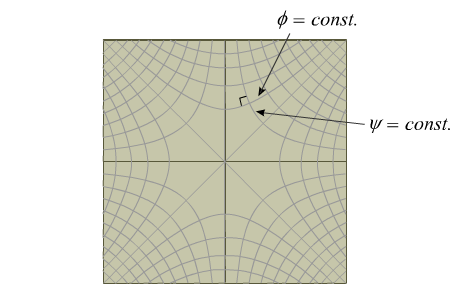
 ふむふむ、等高線をみくらべてみると、それぞれの等高線が直角に交わっているわね。これがさっき出てきたcurvilinear squaresっていうことなのかしら? ふむふむ、等高線をみくらべてみると、それぞれの等高線が直角に交わっているわね。これがさっき出てきたcurvilinear squaresっていうことなのかしら?
 ドクター博士ったら、たまに英語なんか使っちゃって、もしかして西洋かぶれ? ドクター博士ったら、たまに英語なんか使っちゃって、もしかして西洋かぶれ?
 ちがうのよ。作者が日本語をよく知らないだけらしいのよ(笑)。 ちがうのよ。作者が日本語をよく知らないだけらしいのよ(笑)。
 これこれ、何を話しておる? ワシのウワサ話している場合じゃないぞ。さぁ、よーく見つめてみると、φ = (一定) の曲線とψ = (一定) の曲線は90度角度が違うだけで、まったく同じ曲線だってこと、気がつかないかい? これこれ、何を話しておる? ワシのウワサ話している場合じゃないぞ。さぁ、よーく見つめてみると、φ = (一定) の曲線とψ = (一定) の曲線は90度角度が違うだけで、まったく同じ曲線だってこと、気がつかないかい?
 げげ、ほんとだ。 げげ、ほんとだ。
 あ、これひょっとしたら、極座標表示ですっきりするかも。下のようにθとrを使えば、、、 あ、これひょっとしたら、極座標表示ですっきりするかも。下のようにθとrを使えば、、、
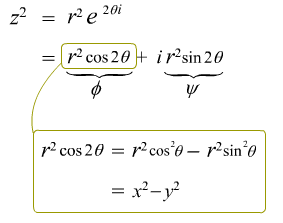
 あ、ほんとだ。x2- y2って cos の二倍角の公式と関連があったのね。そして2xyは sin の二倍角と。そして、φとψが直交するのも当然だわ。 cos と sin でそれぞれあらわされるんだからね。 あ、ほんとだ。x2- y2って cos の二倍角の公式と関連があったのね。そして2xyは sin の二倍角と。そして、φとψが直交するのも当然だわ。 cos と sin でそれぞれあらわされるんだからね。
 ほっほ。だいぶいろいろなことがわかってきてうれしいね。それじゃ、コーシー・リーマンの連立方程式をもう一回みてみよう。それぞれφ =一定の曲線とψ = 一定の曲線について、なにかわかることないかな?ヒントは偏微分の巻でまなんだ、全微分じゃよ。 ほっほ。だいぶいろいろなことがわかってきてうれしいね。それじゃ、コーシー・リーマンの連立方程式をもう一回みてみよう。それぞれφ =一定の曲線とψ = 一定の曲線について、なにかわかることないかな?ヒントは偏微分の巻でまなんだ、全微分じゃよ。
 全微分?よし、それじゃ、さっそく学んだばかりの全微分の式をかきくだしてみましょう。 全微分?よし、それじゃ、さっそく学んだばかりの全微分の式をかきくだしてみましょう。
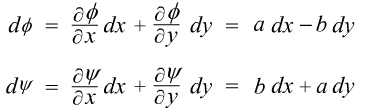
 せっかくコーシー・リーマンの方程式を扱ったわけだから、それぞれの微分係数を a とか b などの定数を用いて表したわ。これがz = z0において成り立つわけね。 せっかくコーシー・リーマンの方程式を扱ったわけだから、それぞれの微分係数を a とか b などの定数を用いて表したわ。これがz = z0において成り立つわけね。
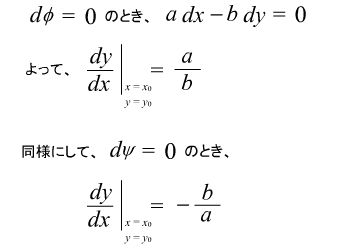
 あれれ、dφ=0のときの曲線の傾きと、dψ= 0 のときの曲線の傾きが垂直になる結論を得るわね。これって、さっき話していたことにつながるんじゃない? あれれ、dφ=0のときの曲線の傾きと、dψ= 0 のときの曲線の傾きが垂直になる結論を得るわね。これって、さっき話していたことにつながるんじゃない?
 あ、ほんとだ。dφ=0を代入するってことは、ある dx と dy のときにφがまったく増えませんってことだよね。それは等高線の方向の (dx,dy) だ。下の図を見てみると、すごくわかりやすいよ。 あ、ほんとだ。dφ=0を代入するってことは、ある dx と dy のときにφがまったく増えませんってことだよね。それは等高線の方向の (dx,dy) だ。下の図を見てみると、すごくわかりやすいよ。
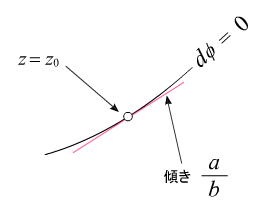
 で、一方、dψ= 0 のときはどうなるかというと、、、 で、一方、dψ= 0 のときはどうなるかというと、、、
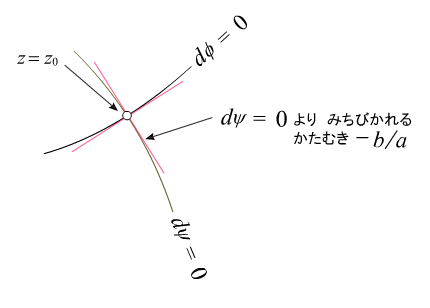
 となって、お互い垂直になるナゾが解けたわね。 となって、お互い垂直になるナゾが解けたわね。
 ふぉっふぉっふぉ。なかなかうまくやっとるじゃないか。これだけ深く掘り下げたら、いつかきっと役にたつぞい。実際、f(z) = z2の曲線は、流体力学でも出てくるぞ。x = 0 と y = 0 の十字で垂直な壁でしきられた流れ、というやつじゃ。ψの等高線を見るとそんなかんじがしないかい? ふぉっふぉっふぉ。なかなかうまくやっとるじゃないか。これだけ深く掘り下げたら、いつかきっと役にたつぞい。実際、f(z) = z2の曲線は、流体力学でも出てくるぞ。x = 0 と y = 0 の十字で垂直な壁でしきられた流れ、というやつじゃ。ψの等高線を見るとそんなかんじがしないかい?
 うんうん、わかる。てことは、dψ = const. の曲線は、一般的に流体が流れる線をあらわしてるってこと?? うんうん、わかる。てことは、dψ = const. の曲線は、一般的に流体が流れる線をあらわしてるってこと??
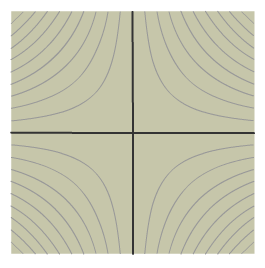
 「流線」とよぶ。ま、今回は複素関数および複素積分を勉強していくわけだから、流体力学には深くは たちいらない。興味があったら、しらべてみよう。 「流線」とよぶ。ま、今回は複素関数および複素積分を勉強していくわけだから、流体力学には深くは たちいらない。興味があったら、しらべてみよう。
 さぁ、次はいよいよ複素積分ね。このページのやりとりが理解できるのであれば、複素積分にはいっても多分だいじょうぶよ。 さぁ、次はいよいよ複素積分ね。このページのやりとりが理解できるのであれば、複素積分にはいっても多分だいじょうぶよ。
 複素積分というと、どういう経路Cを通るのか、そこをきちんと把握しながら進まなくちゃいけない、っていうやつだったっけ。 複素積分というと、どういう経路Cを通るのか、そこをきちんと把握しながら進まなくちゃいけない、っていうやつだったっけ。
 そう、実際は正則であれば、経路がどうであっても構わないんじゃが、まずはそれを感覚的に理解できるようにしてみたぞ。 そう、実際は正則であれば、経路がどうであっても構わないんじゃが、まずはそれを感覚的に理解できるようにしてみたぞ。
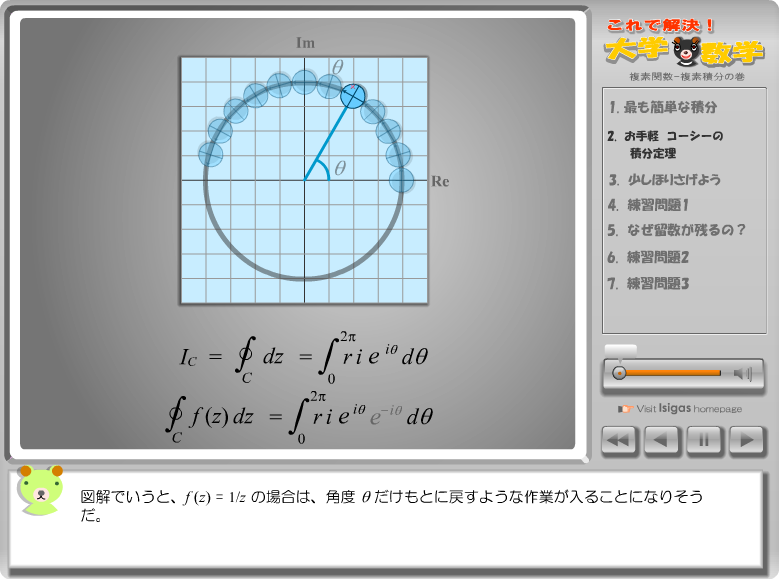
 f(z) = 1/z のような関数では、周回積分するとどうしてゼロにならないか、そこが今回の「複素積分の巻」の主なみどころじゃ。計算式だけじゃなくて、グラフィック解法で解説するから、すいすいと理解できる。 f(z) = 1/z のような関数では、周回積分するとどうしてゼロにならないか、そこが今回の「複素積分の巻」の主なみどころじゃ。計算式だけじゃなくて、グラフィック解法で解説するから、すいすいと理解できる。
 そして、ローラン展開を導入して、さまざまな複素積分が解けるようになるための準備運動をするのね。少しだけでも練習問題を解けるようになったら、あとは普通の教科書をみながらラクに勉強を進めていけそうだわ。 そして、ローラン展開を導入して、さまざまな複素積分が解けるようになるための準備運動をするのね。少しだけでも練習問題を解けるようになったら、あとは普通の教科書をみながらラクに勉強を進めていけそうだわ。
|
 |
   
これで解決!複素積分解説ムービー
(Windowsのみ) 所要時間:40分
対象:
大学生2年以上です。以下のような人が対象です。
・複素関数をすこしだけ学んでみたけれど、複素積分となるとなかなかむずかしい。
・留数とは何かよくわかっていない。
注意:
・偏微分がふんだんに登場しますので、「偏微分の巻」を受講している必要があります。
・eiθが登場します。これがθの角度の回転をあらわすことを把握している必要があります。
・虚数のiが、90度の回転を意味していることを理解している必要があります。
・まずは超簡単な積分からみていきます。ただ単に式を追うだけでなく、「こども座標」なるものを導入して、直感的に理解しやすい工夫をしていきましょう。(無料部分)
・コーシーの積分定理の簡単な証明として、円上の周回積分を解いていきます。
・もうすこし一般的で、しかも数式を用いた解法についてみていきましょう。ストークスの定理やグリーンの定理などと呼ばれたりしていますが、これも図解で解説。
・留数を導入します。これを用いてすぐに問題が解けることを練習問題を解きながら把握していきます。
・留数をもちいた練習問題その2
・積分経路を自分で設定することにより、次の積分を複素積分を用いて解いていきます。
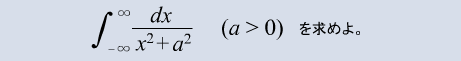
上で示した練習問題が最後の練習問題です。これより奥へは進みませんので、複素積分の発展を学びたい方には適さない可能性があります。
|
 |
 第1章までの無料のムービーはこちらへどうぞ。(音声はありません。) 全てをご覧頂くには、ご購入いただく必要があります。 第1章までの無料のムービーはこちらへどうぞ。(音声はありません。) 全てをご覧頂くには、ご購入いただく必要があります。

クリックして早速見てみよう!
|
 |
 スクリーンショット スクリーンショット



|
|

