|
|
陰関数の基礎
 偏微分－接平面と勾配の巻で、
の意味について学んだね。これを利用して、陰関数による導関数を求めてみよう。じゃあ、さっそく例題を解いてみようか。
 またまた、英語の問題ばっかりだね、Isigasでは(笑)。問題文を読むと、xで微分しろって書いてるよ。"with respect to ~"は「～に関して」っていう意味だね。さて、さっそく考えてみよう、、、、うーむ、これって、両辺をxで微分するだけでしょ？y2の項は、yで微分して 2y とし、そのあとに dy/dx を掛けるから、2y(dy/dx) となるっていう簡単な話じゃないの？
ん、まぁそうなんじゃが、今回はせっかく接平面の式を学んだばっかりだから、それを使って導関数を考えていくぞ。まず、すべての項を左辺に寄せて、それをzと定義しよう。
もちろん問題に与えられた条件式から考えると、 z = 0 から動かしてはいけないのじゃが、今回はすこし動かしたとして、dz を考えてみよう。すると、その増分は
という式で与えられるね。
 あ、わかったわ。まず、この右辺の偏導関数を実際に計算してみましょう。すると、、
となったわ。ここで、dz = 0 が登場するのよ。与えられた問題では、zは常にゼロなんだからね。そうすると、
となって、これを解いて、
となって答えにたどりついたわ。なるほど、いろんなアプローチのしかたによって、さまざまな求め方ができる、っていうのはすばらしいわね。では、次の問題にとりかかってみましょう。
あらいやだ。さっきの練習問題と似ているようで、微妙にちがうのかしら。"vertical tangent"は、「鉛直方向にまっすぐな傾き」だから、dy/dxが -∞ か、 +∞ になるときを考えることになるのかしら。
じゃあ、さっそく解いてみよう。まず dz の式から。
そして、導関数を求めると、、、、
となったよ。かたむきが無限大となるのは、 y = 0 のときだね。このとき、与えられた問題式に再びこの y = 0 を代入することによって、x = 0, -1のふたつを得たよ。こたえは(0,0), (-1,0)のふたつだね。…でも、なんだかあやしい。いじわるなドクター博士のことだから、このままこれで終わるはずがない。
はっはっは。勘がするどいね。かたむきが無限大となるためには y = 0 とならなくてはならないが、y = 0 であれば、かならずかたむきが無限大となるとは限らないよ。分子も分母もある一定の割合でゼロに近づいていくとしたら、dy/dx = 0/0 の構図になるね。
そうか。x→0のとき、yもy→0になるからね。よし、こうなれば裏技よ。グラフ描画ソフトで、問題で与えられていた式を図形化しちゃおう。
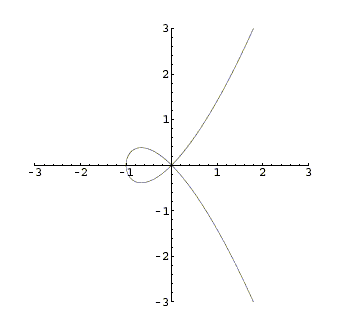
げげ、ずるい～！でも、実際にグラフを見ると一目瞭然だ。原点のところでは、なんと二本の曲線が交わっていたんだね。で、x = -1, y = 0 の解はどうやらただしそうだよ。
原点に近づいていくとき、高次の項は無視できるわよね（下図）。そうすると、問題文で与えられた式から、x = ± yという式が得られるから、グラフ描画ソフトを使わなくても、原点の近くでは、かたむきがそれぞれ1と-1の二本の曲線が交わっていることが分かっていたかもしれないわ、私たちが注意深ければね。
ほんとだね。そもそも、傾きが無限大である点を求める際に、ゼロで割ってはいけない陰関数の定理を用いるっていう時点で、ちょっと無理があったかもしれない。
ほっほっほ。くまきちもみいさんも、いろいろ考えてがんばっているようじゃな。
|
|
|
公開中の授業
